Introduction

Super Learning is a conceptually simple way of combining predictions from different models using cross validation. It simply uses the cross-validated results to form an optimal weighted combination of predictions. Combining predictions across models, typically refered to as stacking or stacked ensembles, is not new. I’ve seen references as far back as about 30 years, though I wouldn’t be surprised if it was much older. However, as far as I know, it was only relatively recently (within 15 years) that some nice theoretical properties were proven for a particular type of stacking called super learning. The paper by Mark van der Laan establishing the results for the super learner can be found here Super Learner by Mark van der Laan.

I learned about super learning by attending a short course at Harvard school of public health led by Dr. Sherri Rose and Dr. Laura Hatfield. Dr. Rose gave a very nice presentation on the super learner and a few examples using it from her own research. The thing that really stood out to me about this method was its unification of the prediction model building process. There is no longer a need to pick a single model as best. This can be particularly difficult if several models perform similarly. The super learner will typically perform as good as the single best performing model and often better. Below I work through building a super learner from scratch.

A few resources I found very helpful for this are Stacked Generalizations by Ashley Naimi and Laura Balzer, the github for the paper, and the github for the SuperLearner package in R. Good chunks of the code below are taken and slightly edited from the Naimi and Balzer github. Additionally, datacamp published a nice article a few days ago walking through the SuperLearner package datacamp. datacamp is a great and cost effective way of learning about programming, statistics, and machine learning. I’ve used it in the past and recommend it, especially for beginners.

Super Learning from Scratch

library(rms)

## Loading required package: Hmisc

## Loading required package: lattice

## Loading required package: survival

## Loading required package: Formula

## Loading required package: ggplot2

## 
## Attaching package: 'Hmisc'

## The following objects are masked from 'package:base':
## 
##     format.pval, units

## Loading required package: SparseM

## 
## Attaching package: 'SparseM'

## The following object is masked from 'package:base':
## 
##     backsolve

library(mvtnorm)
library(Matrix)
library(SuperLearner)

## Loading required package: nnls

## Super Learner

## Version: 2.0-22

## Package created on 2017-07-18

#Randomly generate data
set.seed(1256)

N = 10000
NVAR <- 5
#Covariance Matrix
sigma <- matrix(runif(NVAR^2,0,1), ncol=NVAR)
sigma <- forceSymmetric(sigma)
sigma <- as.matrix(nearPD(sigma)$mat)

#Mean vector: 
mu <- round(runif(NVAR,-1,.1),2)
print(mu)

## [1] -0.46 -0.47 -0.27 -0.94 -0.75

#Generate data
X <- rmvnorm(N, mean=mu, sigma=sigma)
X <- cbind(X,X[,1]^2)
X <- cbind(X,X[,2]*X[,3])


coefs <- round(runif(NVAR+2, -.5, .5),2)
#Outcome
lo <- X %*% coefs
hist(lo)

#Extreme probabilities will make optimization more difficult
pr <- exp(lo)/(1 + exp(lo))

Y <- rbinom(N, size = 1,pr = pr)

Exploring the data

I generated a summary table of the 7 predictor variables as well as a pairs plot. Additionally, I plotted the probability of an event as a function of each predictor variable. The plots show some nice looking relationships, but this is fake data so we won’t dwell on it much. However, it’s always good to exploratory analysis before fitting your models.

#Exploratory plots
summary(X)

##        V1                  V2                V3                V4         
##  Min.   :-3.094573   Min.   :-4.2007   Min.   :-3.9632   Min.   :-4.0099  
##  1st Qu.:-0.903185   1st Qu.:-1.1385   1st Qu.:-0.9596   1st Qu.:-1.4806  
##  Median :-0.460482   Median :-0.4630   Median :-0.2677   Median :-0.9303  
##  Mean   :-0.457468   Mean   :-0.4705   Mean   :-0.2581   Mean   :-0.9285  
##  3rd Qu.:-0.004579   3rd Qu.: 0.1893   3rd Qu.: 0.4380   3rd Qu.:-0.3772  
##  Max.   : 2.393029   Max.   : 3.1435   Max.   : 3.2037   Max.   : 1.9370  
##        V5                V6                V7          
##  Min.   :-4.5139   Min.   :0.00000   Min.   :-3.31823  
##  1st Qu.:-1.3520   1st Qu.:0.07253   1st Qu.:-0.03143  
##  Median :-0.7373   Median :0.32206   Median : 0.24488  
##  Mean   :-0.7367   Mean   :0.66349   Mean   : 0.68102  
##  3rd Qu.:-0.1089   3rd Qu.:0.90247   3rd Qu.: 1.03135  
##  Max.   : 2.9404   Max.   :9.57638   Max.   :13.27604

pairs(X)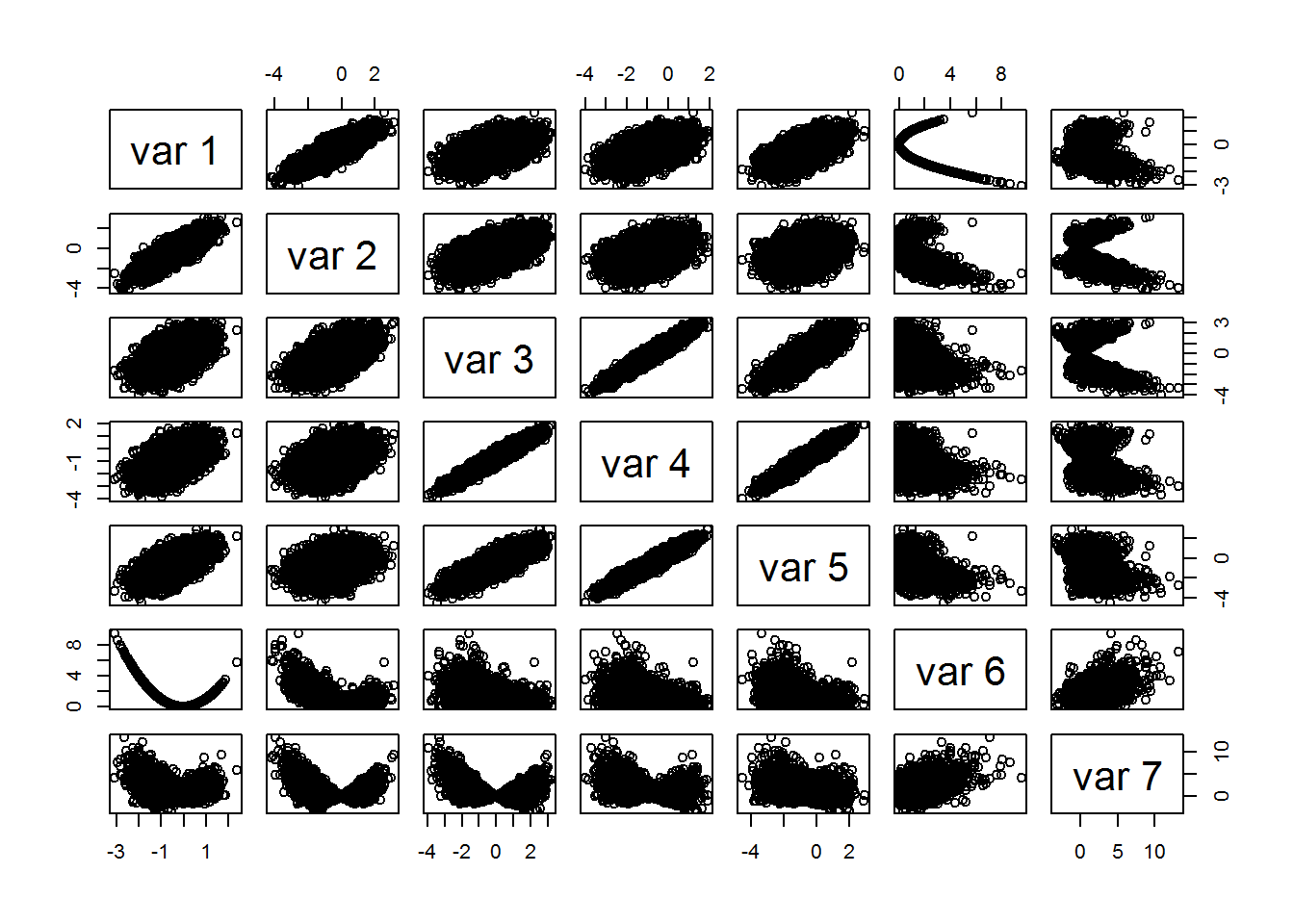

par(mfrow = c(3,3))
invisible(lapply(1:ncol(X), function(i) plot(X[,i],pr)))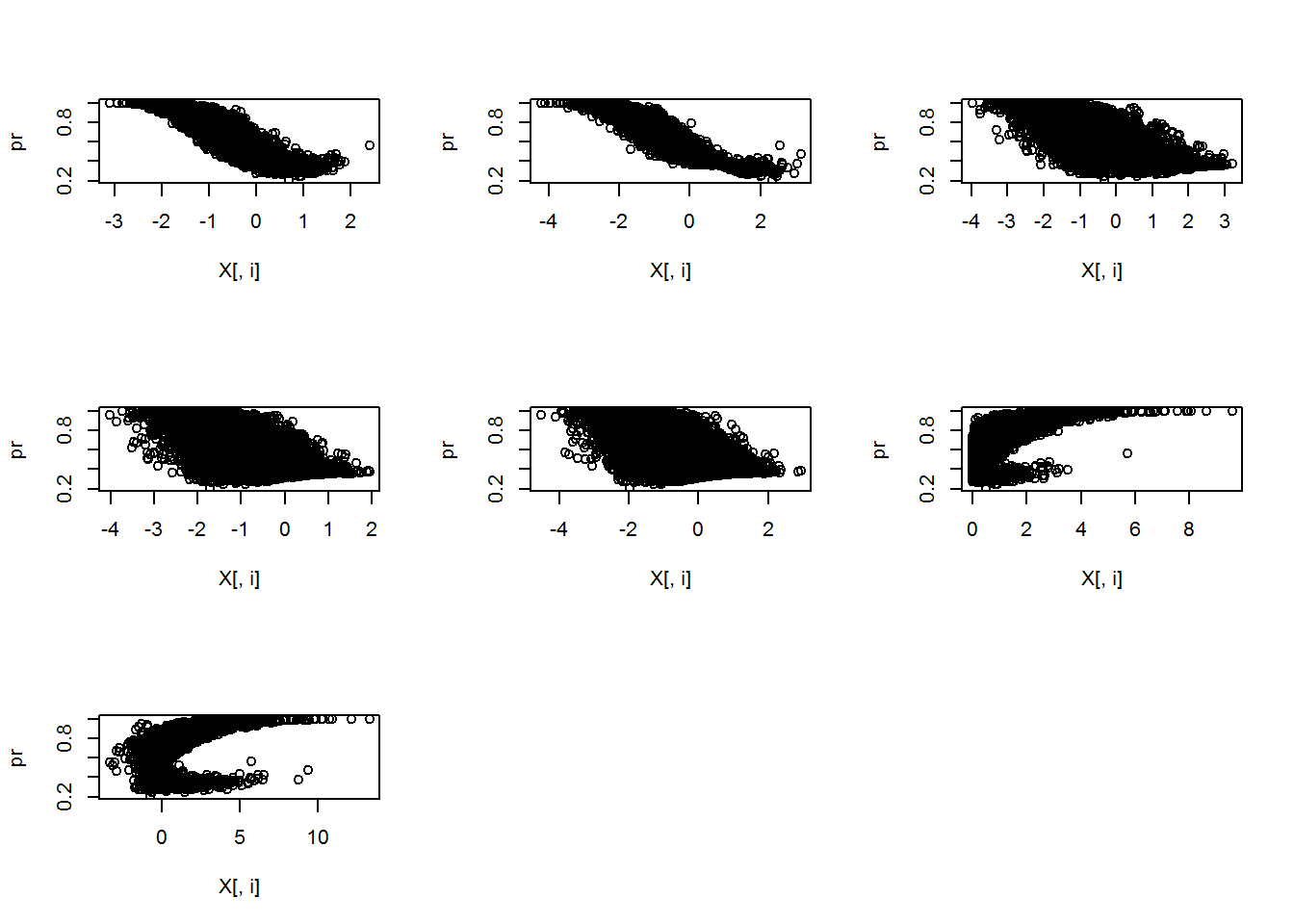

Fitting the super learner using the SuperLearner package

The super learner function syntax is fairly straight forward and similar to fitting any other model. The biggest difference is the SL.library, the list of candidate algorithms for the super learner to build. The package comes with build in wrapper functions (all the models with SL. in from of the name) for a fairly wide variety of models. If you want to use other models, or specify particular tuning parameters, you’ll need to write your own wrapper functions. The datacamp tutorial helpfully covers that.

The candidate models I’m going to use are a main effects glm, linear discriminate analysis (lda), quadratic discriminate analysis (qda), and a random forest (using the ranger package). I fit the super learner twice, each with a separate loss function. The first is rank loss (AUC), while the second is the negative log likelihood. I’m just going to store the results and compare them to what I derive manually. The results we get should be very similar to what the function produces.

#Super Learner

DAT <- data.frame(X[,1:5])

SL.library <- c("SL.glm",
                "SL.lda",
                "SL.qda",
                "SL.ranger")



system.time({
  sl.AUC = SuperLearner(Y = Y, X = DAT,
                    family = binomial(),
                    method = "method.AUC",
                    SL.library = SL.library)
})

## Loading required package: cvAUC

## Loading required package: ROCR

## Loading required package: gplots

## 
## Attaching package: 'gplots'

## The following object is masked from 'package:stats':
## 
##     lowess

## Loading required package: data.table

## 

## cvAUC version: 1.1.0

## Notice to cvAUC users: Major speed improvements in version 1.1.0

## 

## Loading required package: MASS

## Loading required package: ranger

##    user  system elapsed 
##  136.70    1.97  135.03

system.time({
  sl.LL = SuperLearner(Y = Y, X = DAT,
                    family = binomial(),
                    method = "method.NNloglik",
                    SL.library = SL.library)
})

##    user  system elapsed 
##  132.44    1.45  130.37

Manually building the super learner

The super learner is a weighted combination of the cross validated predictions of the candidate models. In the code below I perform 20 fold cross validation for the glm, lda, qda, and random forest models and store the results. I then combine these with the observed outcomes (vector of 1s and 0s) into a 10,000 by 5 matrix. In order to derive the super learner weights, you simply need to optimize your selected loss function. That is, use the optim function in R to find the coefficients that minimize or maximize the loss/objective function. I compute the weights for two loss functions: the rank loss (AUC) and negative log likelihood. I prefer the latter because it’s a proper scoring rule (won’t tell you a worse model is better). The weights are standardized so that they sum to one.

DATA <- data.frame(Y = Y, DAT)


#Create folds
folds <- 20
splt <- split(DATA,1:folds)


#Fit models
glm.mods <- lapply(1:folds, function(ii) glm(formula = Y ~ ., data = do.call(rbind, splt[-ii]), family="binomial"))
lda.mods <- lapply(1:folds, function(ii) lda(formula = Y ~ ., data = do.call(rbind, splt[-ii])))
qda.mods <- lapply(1:folds, function(ii) qda(formula = Y ~ ., data = do.call(rbind, splt[-ii])))
rf.mods <- lapply(1:folds, function(ii) ranger(formula = Y ~ ., data = do.call(rbind, splt[-ii])))

#Compute model Predictions

p.glm <- lapply(1:folds,function(ii) predict(glm.mods[[ii]], newdata = rbindlist(splt[ii]), type = "response"))
p.lda <- lapply(1:folds,function(ii) predict(lda.mods[[ii]], newdata = rbindlist(splt[ii]), type = "response"))
p.qda <- lapply(1:folds,function(ii) predict(qda.mods[[ii]], newdata = rbindlist(splt[ii]), type = "response"))
p.rf <- lapply(1:folds,function(ii) predict(rf.mods[[ii]], data = rbindlist(splt[ii]), type = "response"))


#Combine outcomes with prediction probabilities
Y.preds <- NULL
for(i in 1:folds){
  Y.preds[[i]]<-cbind(splt[[i]][,1],p.glm[[i]],p.lda[[i]]$posterior[,2],p.qda[[i]]$posterior[,2], p.rf[[i]]$predictions)
}


#Manually compute SL coefficients

cv.X <- data.frame(do.call(rbind,Y.preds),row.names=NULL); names(X)<-c("Y","GLM","LDA","QDA","RF")

bounds = c(0, Inf)

AUCF<-function(A, y, par){
  AUCC <- function(A,y,par) {
  A<-as.matrix(A)
  names(par)<-c("GLM","LDA","QDA","RF")
  predictions <- crossprod(t(A),par)
  1 - AUC(predictions = predictions, labels = y)
  }
  bounds = c(0, Inf)
  fit <- optim(par= par, fn=AUCC, A=A, y=y,
               method="L-BFGS-B",lower=bounds[1],upper=bounds[2])
  fit$par/sum(fit$par)
  
}

##Binomial negative log likelihood
NNloglik <- function(A, y, par) {
  A <- as.matrix(trimLogit(A, trim = 0.001))
  names(par) <- c("GLM","LDA","QDA","RF")
  fmin <- function(par, A, y) {
    p <- plogis(crossprod(t(A), par))
   -sum(2 * ifelse(y, log(p), log(1-p)))
  }
  gmin <- function(par, A, y) {
    names(par) <- c("GLM","LDA","QDA","RF")
    eta <- A %*% par
    p <- plogis(eta)
    -2 * t(dlogis(eta) * ifelse(y, 1/p, -1/(1-p))) %*% A
  }
  fit2 <- optim(par, fn = fmin, gr = gmin, A = A, y = y, method = "L-BFGS-B", lower = 0)
  fit2$par[fit2$par < 0] <- 0
  fit2$par[is.na(fit2$par)] <- 0
  print(fit2)
  print(fit2$par/sum(abs(fit2$par)))
}  

Comparing manual weights with SuperLearner function weights

We can see that there are slight differences between the manual super learner weights and the weights from the function, but that they are overall fairly close.

#AUC Results
sl.AUC

## 
## Call:  
## SuperLearner(Y = Y, X = DAT, family = binomial(), SL.library = SL.library,  
##     method = "method.AUC") 
## 
## 
##                    Risk      Coef
## SL.glm_All    0.2750461 0.3337970
## SL.lda_All    0.2750400 0.3357307
## SL.qda_All    0.2753354 0.3304723
## SL.ranger_All 0.3241119 0.0000000

AUCF(cv.X[,2:5], cv.X[,1], par = c(1/4,1/4,1/4,1/4))

## [1] 0.3361015 0.3304125 0.3334860 0.0000000

##Log likelihood Results
sl.LL  

## 
## Call:  
## SuperLearner(Y = Y, X = DAT, family = binomial(), SL.library = SL.library,  
##     method = "method.NNloglik") 
## 
## 
##                    Risk Coef
## SL.glm_All    0.5931421    0
## SL.lda_All    0.5931418    0
## SL.qda_All    0.5889857    1
## SL.ranger_All       Inf    0

NNloglik(par = c(1/4,1/4,1/4,1/4), A = cv.X[,2:5], y = cv.X[,1])

## $par
##      GLM      LDA      QDA       RF 
## 0.000000 0.000000 1.004494 0.000000 
## 
## $value
## [1] 11776.67
## 
## $counts
## function gradient 
##       12       12 
## 
## $convergence
## [1] 0
## 
## $message
## [1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"
## 
## GLM LDA QDA  RF 
##   0   0   1   0